CAVS / Capabilities / Materials Modeling / ICME / Internal State Variable Thermoplastic

Integrated Computational Materials Engineering (ICME)

Thermoplastic Internal State Variable (ISV) model

The Mississippi State University Internal State Variable (ISV) model for thermoplastics, polymers and soft tissue. This hyper-elastic visco-plastic material model was developed in 2010 as presented in Bouvard et al.[1] and is based on molecular dynamics simulations of entangled polymers. This polymer-based ISV model is able to capture the history effects of a thermoplastic polymer tested under different stress states and strain rates. The modeling approach follows current methodologies used for metals and uses state variables related to microstructural phenomena to determine macroscale behavior considering its thermodynamics. Thus, the material departs from spring-dashpot based models generally used to predict the mechanical behavior of polymers. To select the internal state variables, we have used a hierarchical multiscale approach for bridging mechanisms from the molecular scale (see Atomistic Deformation of Amorphous Polyethylene) to the continuum scale. The continuum constitutive model applied a formalism using a three-dimensional large deformation kinematics and thermodynamics framework. The 3D constitutive equations of the model were implemented in ABAQUS Explicit using a VUMAT subroutine. These equations were then simplified to the one-dimensional case in order to fit the model parameters using MATLAB software.

The TP-ISV material model considers a material with entangled chains at the lower length scale. The effect of this microstructure at the macroscale is described by three physics based state variables that determine the entanglement effect of the polymer chains (ξ ̅_1), strain induced crystallization at large strains (ξ ̅_2), and chain alignment at large strains (E ̅^β ̅ ). Figure 1 shows the generality of these state variables in the stress strain behavior of the polymer.


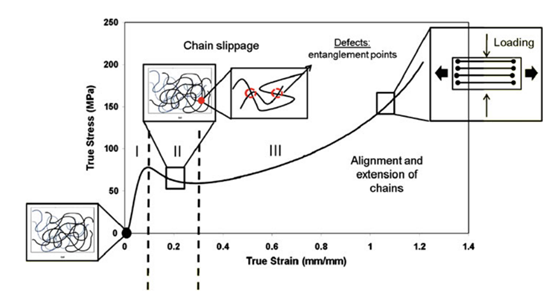
Figure 1. Response of an amorphous polymer under compression for temperatures below the glass transition temperature (Bouvard et al.).

Figure 1. Response of an amorphous polymer under compression for temperatures below the glass transition temperature (Bouvard et al.[1]).

Table 1. Summary of TP-ISV material model equations (Bouvard et al.).

Table 1. Summary of TP-ISV material model equations ( Bouvard et al.[1]).

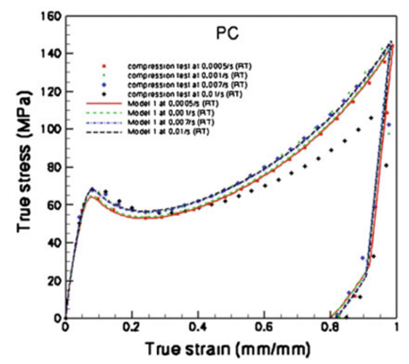
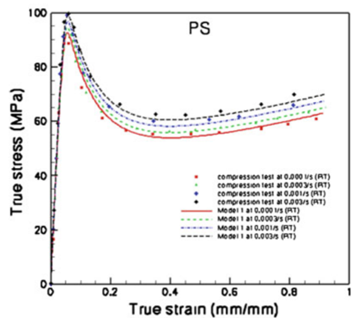
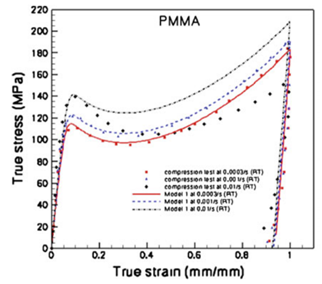
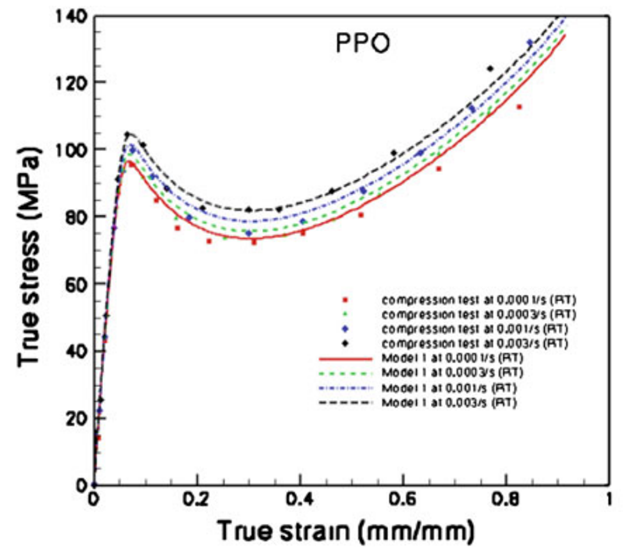
Figure 2. experimental and TP-ISV modeled stress strain curves of polymers at different strain rates Figure 2. experimental and TP-ISV modeled stress strain curves of polymers at different strain rates
Figure 2. experimental and TP-ISV modeled stress strain curves of polymers at different strain rates Figure 2. experimental and TP-ISV modeled stress strain curves of polymers at different strain rates

Figure 2. experimental and TP-ISV modeled stress strain curves of polymers at different strain rates.




The material model has been used to model the rate dependent behavior of polycarbonate (PC), poly(methylmethacrylate) (PMMA), polystyrene (PS), and poly(2,6-dimethyl-1,4-phenylene oxide) (PPO) under large deformations as shown in figure 2. This material model has also been successfully used to model soft tissue behavior at high deformation rates (Prabhu et al.[2]).

The results of an example study are available here: Finite Element Modeling for Biological Materials

References

1.↑Bouvard, J. L., Ward, D. K., Hossain, D., Marin, E. B., Bammann, D. J., & Horstemeyer, M. F. (2010). A general inelastic internal state variable model for amorphous glassy polymers. Acta Mechanica, 213(1–2), 71–96. https://doi.org/10.1007/s00707-010-0349-y

2.↑Prabhu, R., Horstemeyer, M. F., Tucker, M. T., Marin, E. B., Bouvard, J. L., Sherburn, J. A., Liao, J., & Williams, L. N. (2011). Coupled experiment/finite element analysis on the mechanical response of porcine brain under high strain rates. Journal of the Mechanical Behavior of Biomedical Materials, 4(7), 1067–1080.https://doi.org/10.1016/j.jmbbm.2011.03.015