Integrated Computational Materials Engineering (ICME)
Uniaxial Tension
Abstract
This example script shows how to run an atomistic simulation of uniaxial tensile loading of an aluminum single crystal oriented in the <100> direction. This example uses a parallel molecular dynamics code, LAMMPS[1]. These scripts were initially used to study dislocation nucleation in single crystal aluminum and copper[2][3][4].
Author(s): Mark A. Tschopp, mtschopp@cavs.msstate.edu
Input
Description of Simulation
This molecular dynamics simulation first generates a simulation cell with fcc atoms with <100> orientations in the x, y, and z-directions. For this example, the simulation cell size is 10 lattice units in each direction, i.e., 4000 total atoms. Larger simulation cell sizes should be used to converge the dislocation nucleation stress values and to not influence the dislocation nucleation mechanism. The potential used here is the Mishin et al. (1999) aluminum potential[5]. The equilibration step allows the lattice to expand to a temperature of 300 K with a pressure of 0 bar at each simulation cell boundary. Then, the simulation cell is deformed in the x-direction at a strain rate of 1010 1/s, while the lateral boundaries are controlled using the NPT equations of motion to zero pressure. The stress and strain values are output to a separate file, which can be imported in a graphing application for plotting. The cfg dump files include the x, y, and z coordinates, the centrosymmetry values, the potential energies, and forces for each atom. This can be directly visualized using AtomEye[6].
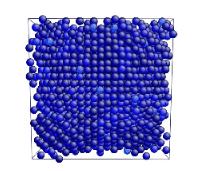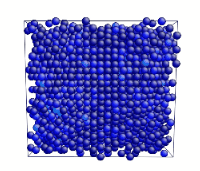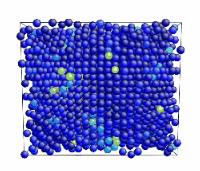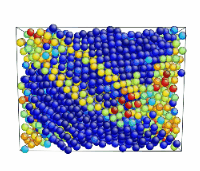
Tensile Loading of an Aluminum Single Crystal. Movie showing deformation of single crystal aluminum loaded in the <100> direction at a strain rate of 1010 s-1 and a temperature of 300 K.
LAMMPS input script
This input script was run using the Aug 2015 version of LAMMPS. Changes in some commands in more recent versions may require revision of the input script. To run this script, store it in "in.tensile.txt" and then use "lmp_exe < in.tensile.txt" in a UNIX environment where "lmp_exe" refers to the LAMMPS executable.
# Input file for uniaxial tensile loading of single crystal aluminum
# Mark Tschopp, November 2010
# ------------------------ INITIALIZATION ----------------------------
units metal
dimension 3
boundary p p p
atom_style atomic
variable latparam equal 4.05
# ----------------------- ATOM DEFINITION ----------------------------
lattice fcc ${latparam}
region whole block 0 10 0 10 0 10
create_box 1 whole
lattice fcc ${latparam} orient x 1 0 0 orient y 0 1 0 orient z 0 0 1
create_atoms 1 region whole
# ------------------------ FORCE FIELDS ------------------------------
pair_style eam/alloy
pair_coeff * * Al99.eam.alloy Al
# ------------------------- SETTINGS ---------------------------------
compute csym all centro/atom fcc
compute peratom all pe/atom
######################################
# EQUILIBRATION
reset_timestep 0
timestep 0.001
velocity all create 300 12345 mom yes rot no
fix 1 all npt temp 300 300 1 iso 0 0 1 drag 1
# Set thermo output
thermo 1000
thermo_style custom step lx ly lz press pxx pyy pzz pe temp
# Run for at least 10 picosecond (assuming 1 fs timestep)
run 20000
unfix 1
# Store final cell length for strain calculations
variable tmp equal "lx"
variable L0 equal ${tmp}
print "Initial Length, L0: ${L0}"
######################################
# DEFORMATION
reset_timestep 0
fix 1 all npt temp 300 300 1 y 0 0 1 z 0 0 1 drag 1
variable srate equal 1.0e10
variable srate1 equal "v_srate / 1.0e12"
fix 2 all deform 1 x erate ${srate1} units box remap x
# Output strain and stress info to file
# for units metal, pressure is in [bars] = 100 [kPa] = 1/10000 [GPa]
# p2, p3, p4 are in GPa
variable strain equal "(lx - v_L0)/v_L0"
variable p1 equal "v_strain"
variable p2 equal "-pxx/10000"
variable p3 equal "-pyy/10000"
variable p4 equal "-pzz/10000"
fix def1 all print 100 "${p1} ${p2} ${p3} ${p4}" file Al_SC_100.def1.txt screen no
# Use cfg for AtomEye
dump 1 all cfg 250 dump.tensile_*.cfg mass type xs ys zs c_csym c_peratom fx fy fz
dump_modify 1 element Al
# Display thermo
thermo 1000
thermo_style custom step v_strain temp v_p2 v_p3 v_p4 ke pe press
run 20000
######################################
# SIMULATION DONE
print "All done"
Output
LAMMPS logfile
The log.lammps file should look like this below. Notice that the 20 ps (20,000 fs) equilibration step brought the temperature of the simulation cell up to 300 K. The corresponding deformation went up to a strain of 0.2. The thermo command was set for every 1000 timesteps, so any plots should be made from the data included in the datafile.
LAMMPS (5 Nov 2010)
# Input file for uniaxial tensile loading of single crystal aluminum
# Mark Tschopp, November 2010
# ------------------------ INITIALIZATION ----------------------------
units metal
dimension 3
boundary p p p
atom_style atomic
variable latparam equal 4.05
# ----------------------- ATOM DEFINITION ----------------------------
lattice fcc ${latparam}
lattice fcc 4.05
Lattice spacing in x,y,z = 4.05 4.05 4.05
region whole block 0 10 0 10 0 10
create_box 1 whole
Created orthogonal box = (0 0 0) to (40.5 40.5 40.5)
2 by 2 by 2 processor grid
region upper block INF INF INF INF INF INF units box
lattice fcc ${latparam} orient x 1 0 0 orient y 0 1 0 orient z 0 0 1
lattice fcc 4.05 orient x 1 0 0 orient y 0 1 0 orient z 0 0 1
Lattice spacing in x,y,z = 4.05 4.05 4.05
create_atoms 1 region upper
Created 4000 atoms
# ------------------------ FORCE FIELDS ------------------------------
pair_style eam/alloy
pair_coeff * * Al99.eam.alloy Al
# ------------------------- SETTINGS ---------------------------------
compute csym all centro/atom fcc
compute peratom all pe/atom
######################################
# EQUILIBRATION
reset_timestep 0
timestep 0.001
velocity all create 300 12345 mom yes rot no
fix 1 all npt temp 300 300 1 iso 0 0 1 drag 1
# Set thermo output
thermo 1000
thermo_style custom step lx ly lz press pxx pyy pzz pe temp
# Run for at least 10 picosecond (assuming 1 fs timestep)
run 20000
Memory usage per processor = 2.55571 Mbytes
Step Lx Ly Lz Press Pxx Pyy Pzz PotEng Temp
0 40.5 40.5 40.5 2496.1233 2446.9902 2534.6541 2506.7256 -13440 300
1000 40.558342 40.558342 40.558342 731.50829 755.55351 696.37101 742.60035 -13363.301 169.49172
2000 40.574199 40.574199 40.574199 106.78935 -46.253007 296.26883 70.352219 -13356.097 178.17311
3000 40.579471 40.579471 40.579471 314.81803 314.71612 292.22553 337.51245 -13347.025 183.623
4000 40.586697 40.586697 40.586697 107.84524 52.829414 112.73441 157.9719 -13340.823 194.61149
5000 40.593224 40.593224 40.593224 172.67874 158.86784 199.13978 160.02861 -13334.364 204.85854
6000 40.601567 40.601567 40.601567 56.953653 -6.2830484 -16.301111 193.44512 -13327.55 213.93605
7000 40.60782 40.60782 40.60782 31.891969 35.437938 63.396951 -3.1589825 -13320.86 222.48071
8000 40.616908 40.616908 40.616908 -244.41321 -212.11716 -305.70692 -215.41555 -13317.384 236.254
9000 40.618876 40.618876 40.618876 13.561356 111.07353 -29.999797 -40.389663 -13313.071 247.18002
10000 40.625506 40.625506 40.625506 -125.06329 -105.4566 -93.514599 -176.21866 -13308.875 256.93613
11000 40.631525 40.631525 40.631525 -75.690987 141.36136 14.068057 -382.50238 -13303.582 263.00631
12000 40.631815 40.631815 40.631815 79.38005 63.796397 144.76416 29.579595 -13299.23 269.23326
13000 40.637408 40.637408 40.637408 -152.9113 -399.37081 -31.484802 -27.878283 -13298.162 280.0582
14000 40.636962 40.636962 40.636962 237.09239 58.799334 196.78768 455.69014 -13294.166 283.43969
15000 40.641455 40.641455 40.641455 105.44503 114.55343 142.4659 59.315739 -13291.527 287.73561
16000 40.643072 40.643072 40.643072 82.986611 -130.36308 288.9926 90.330318 -13288.384 289.39655
17000 40.64789 40.64789 40.64789 -12.310673 -112.67891 -132.8659 208.6128 -13289.081 296.89271
18000 40.644319 40.644319 40.644319 269.36896 180.82571 218.97472 408.30644 -13286.862 297.25615
19000 40.646772 40.646772 40.646772 166.57104 20.881491 -79.807885 558.63952 -13287.577 301.80321
20000 40.649126 40.649126 40.649126 116.57534 -108.86953 156.54682 302.04873 -13284.646 298.01867
Loop time of 81.5242 on 8 procs for 20000 steps with 4000 atoms
Pair time (%) = 64.1903 (78.7378)
Neigh time (%) = 0 (0)
Comm time (%) = 13.9448 (17.1051)
Outpt time (%) = 0.00286543 (0.00351483)
Other time (%) = 3.38623 (4.15365)
Nlocal: 500 ave 500 max 500 min
Histogram: 8 0 0 0 0 0 0 0 0 0
Nghost: 2930 ave 2930 max 2930 min
Histogram: 8 0 0 0 0 0 0 0 0 0
Neighs: 35000 ave 36430 max 33540 min
Histogram: 2 0 1 1 0 0 1 1 0 2
FullNghs: 0 ave 0 max 0 min
Histogram: 8 0 0 0 0 0 0 0 0 0
Total # of neighbors = 280000
Ave neighs/atom = 70
Neighbor list builds = 0
Dangerous builds = 0
unfix 1
# Store final cell length for strain calculations
variable tmp equal "lx"
variable L0 equal ${tmp}
variable L0 equal 40.64912642
print "Initial Length, L0: ${L0}"
Initial Length, L0: 40.64912642
######################################
# DEFORMATION
reset_timestep 0
fix 1 all npt temp 300 300 1 y 0 0 1 z 0 0 1 drag 1
variable srate equal 1.0e10
variable srate1 equal "v_srate / 1.0e12"
fix 2 all deform 1 x erate ${srate1} units box remap x
fix 2 all deform 1 x erate 0.01 units box remap x
# Output strain and stress info to file
# for units metal, pressure is in [bars] = 100 [kPa] = 1/10000 [GPa]
# p2, p3, p4 are in GPa
variable strain equal "(lx - v_L0)/v_L0"
variable p1 equal "v_strain"
variable p2 equal "-pxx/10000"
variable p3 equal "-pyy/10000"
variable p4 equal "-pzz/10000"
fix def1 all print 100 "${p1} ${p2} ${p3} ${p4}" file Al_SC_100.def1.txt screen no
# Use cfg for AtomEye
dump 1 all cfg 250 dump.tensile_*.cfg id type xs ys zs c_csym c_peratom fx fy fz
dump_modify 1 element Al
# Display thermo
thermo 1000
thermo_style custom step v_strain temp v_p2 v_p3 v_p4 ke pe press
run 20000
Memory usage per processor = 2.8622 Mbytes
Step strain Temp p2 p3 p4 KinEng PotEng Press
0 -8.7965858e-11 298.01867 0.010886953 -0.015654682 -0.030204873 154.04923 -13284.646 116.57534
1000 0.0099999999 301.40099 0.67990399 0.067064258 0.0053203864 155.79758 -13283.836 -2507.6288
2000 0.02 298.01046 1.2830198 0.019592784 -0.036714858 154.04498 -13276.743 -4219.6592
3000 0.03 304.39575 1.9202839 0.064889677 0.016160978 157.34561 -13271.94 -6671.115
4000 0.04 293.49046 2.5079447 -0.011621532 -0.045248722 151.70854 -13255.553 -8170.2481
5000 0.05 299.61448 3.1080399 -0.0063053351 -0.001951119 154.87412 -13245.404 -10332.611
6000 0.06 301.13685 3.7262713 -0.018319706 0.058027821 155.66105 -13230.48 -12553.265
7000 0.07 304.50008 4.3068752 0.036084841 0.022188973 157.39954 -13214.12 -14550.497
8000 0.08 301.24768 4.8543157 -0.0043461496 0.0099095843 155.71833 -13192.071 -16199.597
9000 0.09 295.90445 5.3741975 -0.0084256638 -0.013966722 152.95636 -13166.694 -17839.35
10000 0.1 292.31188 5.8552584 -0.023696478 -0.020282681 151.09932 -13139.944 -19370.931
11000 0.11 298.84284 6.4501419 0.017547204 0.015913195 154.47525 -13116.23 -21612.008
12000 0.12 295.8812 6.918376 -0.027979731 0.033011555 152.94434 -13085.401 -23078.026
13000 0.13 296.6501 7.4105164 0.040017275 0.063746831 153.3418 -13054.406 -25047.602
14000 0.14 291.84214 7.7838516 0.010140057 -0.050282654 150.85651 -13018.661 -25812.363
15000 0.15 290.68698 7.9945223 0.04870559 0.076553482 150.25939 -12983.262 -27065.938
16000 0.16 377.39464 2.6003776 0.022766694 0.0045660696 195.07956 -13008.794 -8759.0346
17000 0.17 412.37758 1.2494147 -0.0087695036 0.018247454 213.16264 -13041.345 -4196.3088
18000 0.18 429.78685 0.95088514 -0.078803047 0.051915067 222.16169 -13073.821 -3079.9905
19000 0.19 427.62458 0.98387526 0.017524712 0.053337669 221.04399 -13096.987 -3515.7922
20000 0.2 410.07663 1.1025637 0.010470766 -0.082932084 211.97325 -13109.962 -3433.6746
Loop time of 96.4415 on 8 procs for 20000 steps with 4000 atoms
Pair time (%) = 74.4147 (77.1605)
Neigh time (%) = 0.131499 (0.136351)
Comm time (%) = 13.7462 (14.2534)
Outpt time (%) = 2.21778 (2.29961)
Other time (%) = 5.93133 (6.15019)
Nlocal: 500 ave 517 max 489 min
Histogram: 1 2 0 1 1 2 0 0 0 1
Nghost: 2457.88 ave 2466 max 2437 min
Histogram: 1 0 0 0 0 1 1 1 1 3
Neighs: 34511 ave 35305 max 33225 min
Histogram: 1 1 0 1 0 0 0 1 0 4
FullNghs: 69094.8 ave 71637 max 67679 min
Histogram: 2 1 0 1 2 1 0 0 0 1
Total # of neighbors = 552758
Ave neighs/atom = 138.19
Neighbor list builds = 67
Dangerous builds = 0
######################################
# SIMULATION DONE
print "All done"
All done
LAMMPS datafile
The following datafile was also generated during this simulation.
# Fix print output for fix def1 0.0009999999119 0.08667300618 0.03175758225 0.03801213452 0.001999999912 0.09131420312 -0.05499624531 -0.03396621651 0.002999999912 0.2254889267 0.04825004506 0.04680554658 0.003999999912 0.2199842183 -0.04156649661 -0.02074145126 0.004999999912 0.3127067321 0.01435171918 0.01093418588 ...
LAMMPS dumpfile
The following dumpfile in cfg format was also generated during this simulation.
Number of particles = 4000 A = 1.0 Angstrom (basic length-scale) H0(1,1) = 40.6491 A H0(1,2) = 0 A H0(1,3) = 0 A H0(2,1) = 0 A H0(2,2) = 40.6491 A H0(2,3) = 0 A H0(3,1) = 0 A H0(3,2) = 0 A H0(3,3) = 40.6491 A .NO_VELOCITY. entry_count = 8 auxiliary[0] = csym auxiliary[1] = peratom auxiliary[2] = fx auxiliary[3] = fy auxiliary[4] = fz 26.982 Al 0.0493442 0.0581882 0.00323696 1.58804 -3.34266 0.196691 -0.804728 -0.0280286 0.0987502 0.00417997 0.00238952 0.827133 -3.34273 -0.475844 -0.270217 -0.120716 0.0989802 0.0523976 0.0521907 0.363772 -3.30304 -0.309005 -0.274515 -0.299433 0.0495058 0.102418 0.0536544 0.611128 -3.30518 0.162097 -0.42069 -0.15808 0.0995051 0.102793 0.00119416 0.614289 -3.28181 -0.406727 -0.192102 0.405813 0.0473774 0.0488825 0.10204 0.581043 -3.3709 0.135458 -0.205472 -0.294232 0.0989535 0.000697083 0.0977144 0.583569 -3.30702 -0.474259 0.0845695 0.400838 ...
POST-PROCESSING
Stress-Strain Plot
The stress-strain curve in Figure 1 can be generated using the following MATLAB script:
%% Analyze def1.txt files
% Plot the various responses
d = dir('*.def1.txt');
for i = 1:length(d)
% Get data
fname = d(i).name;
A = importdata(fname);
strain = A.data(:,1);
stress = A.data(:,2:4);
% Generate plot
plot(strain,stress(:,1),'-or','LineWidth',2,'MarkerEdgeColor','r',...
'MarkerFaceColor','r','MarkerSize',5),hold on
plot(strain,stress(:,2),'-ob','LineWidth',2,'MarkerEdgeColor','b',...
'MarkerFaceColor','b','MarkerSize',5),hold on
plot(strain,stress(:,3),'-og','LineWidth',2,'MarkerEdgeColor','g',...
'MarkerFaceColor','g','MarkerSize',5),hold on
axis square
ylim([0 10])
set(gca,'LineWidth',2,'FontSize',24,'FontWeight','normal','FontName','Times')
set(get(gca,'XLabel'),'String','Strain','FontSize',32,'FontWeight','bold','FontName','Times')
set(get(gca,'YLabel'),'String','Stress (GPa)','FontSize',32,'FontWeight','bold','FontName','Times')
set(gcf,'Position',[1 1 round(1000) round(1000)])
% Export figure to tif file
exportfig(gcf,strrep(fname,'.def1.txt','.tif'),'Format','tiff',...
'Color','rgb','Resolution',300)
close(1)
end
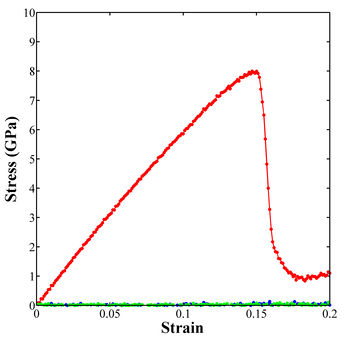
Figure 1. Stress-strain curve for uniaxial tensile loading of single crystal aluminum in the <100> loading direction.
The exportfig command refers to a script on MATLAB Central File website. You will need to go to the website and download the script into the current directory for this to work.
Deformation Movie
First download AtomEye.- Go to AtomEye website.
- Download the A.i686 version by right-clicking on the link and "Save Target As..." to one of your directories.
- Rename the downloaded file as A by typing "cp A.i686 A". A will be the executable.
- Using UNIX, run "chmod A 755" on the file to change this to an executable.
- To test, you need to save a CFG file as well, such as cnt8x3.cfg. Try running using "./A cnt8x3.cfg".
- Go to ImageJ website.
- Download the appropriate version for Windows, LINUX, or MAC.
- Visualize the dumpfile in AtomEye by typing the following command, "/A dump.tensile_0.cfg" (UNIX).
- Use the AtomEye options to select how you want to visualize deformation. In this example, the centrosymmetry parameter was used to show only atoms in a non-centrosymmetric environment (see Fig. 2).
- Use Alt+0 to activate centrosymmetric (csym) view.
- Adjust threshold, or set of atoms to view, by using Shift+T. This will allow creation of a set for the current parameter (in this case, csym). Please note that you need to adjust both lower and higher thresholds unless the atoms from following images that exceeds maximum value for the first one will be not shown. You can make it 5 or 10.
- Make atoms with values outside of the threshold invisible by using Ctrl+A.
- Press 'y' within AtomEye to produce an animation script.
- The folder "Jpg" now contains snapshots of all dumpfiles.
- Open ImageJ
- Drag the folder Jpg into ImageJ
- Select "Convert to RGB" to keep the color from the AtomEye images.
- Choose "yes" to load a stack.
- Adjust the size as needed (Image/Adjust/Size)
- Adjust frame rate as desired (Image/Stacks/Tools/Animation Options)
- Save as Animated Gif file
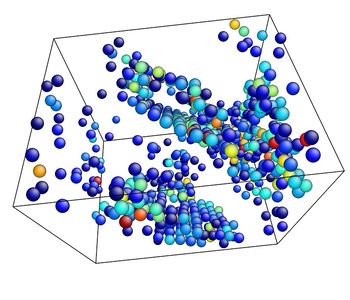
Figure 2. Image of nucleated dislocation near peak stress.
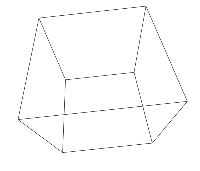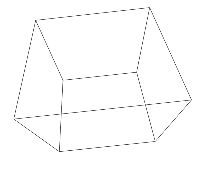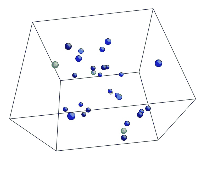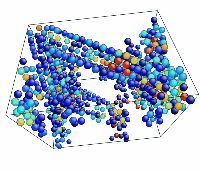
Tensile Loading of an Aluminum Single Crystal. Movie showing deformation of single crystal aluminum loaded in the <100> direction at a strain rate of 1010 s-1 and a temperature of 300 K. Only atoms in non-centrosymmetric environment are shown.
Questions and Answers?
Q1: I ran this tutorial of an atomistic simulation of uniaxial tensile loading of an aluminum single crystal oriented in the <100> direction. However, I want to use the LJ potential instead of the EAM potential. When I run the input script with the Lennard Jones potential, I get much different results. The stress is nearly 3 times the stress from the EAM potential. I don't know where something is wrong.
A1: Interatomic potentials play a commanding role in the properties of molecular dynamics simulations. The most simple potential is the Lennard Jones potential. The embedded atom method potential is a little more sophisticated and I would encourage you to look up the original papers by Mike Baskes (1983, 1984) to examine how this common potential formulation was created. While there are an increasing number of potential formulations out there now and an increasing number of potentials, the embedded atom method has been widely used over the years and still is. However, this brings up the point that different potentials may give vastly different properties because each potential may have been formulated for a particular problem. It is up to the user to decide whether the potential seems to give plausible results for their application or whether the initial fitting contains properties that are important for their application.
Acknowledgements
The authors would like to acknowledge funding for this work through the Department of Energy.
References
- ↑ S. Plimpton, "Fast Parallel Algorithms for Short-Range Molecular Dynamics," J. Comp. Phys., 117, 1-19 (1995).
- ↑ Spearot, D.E., Tschopp, M.A., Jacob, K.I., McDowell, D.L., "Tensile strength of <100> and <110> tilt bicrystal copper interfaces," Acta Materialia 55 (2007) p. 705-714 (http://dx.doi.org/10.1016/j.actamat.2006.08.060).
- ↑ Tschopp, M.A., Spearot, D.E., McDowell, D.L., "Atomistic simulations of homogeneous dislocation nucleation in single crystal copper," Modelling and Simulation in Materials Science and Engineering 15 (2007) 693-709 (http://dx.doi.org/10.1088/0965-0393/15/7/001).
- ↑ Tschopp, M.A., McDowell, D.L., "Influence of single crystal orientation on homogeneous dislocation nucleation under uniaxial loading," Journal of Mechanics and Physics of Solids 56 (2008) 1806-1830. (http://dx.doi.org/10.1016/j.jmps.2007.11.012).
- ↑ Y. Mishin, D. Farkas, M.J. Mehl, and D.A. Papaconstantopoulos, "Interatomic potentials for monoatomic metals from experimental data and ab initio calculations," Phys. Rev. B 59, 3393 (1999).
- ↑ J. Li, "AtomEye: an efficient atomistic configuration viewer," Modelling Simul. Mater. Sci. Eng. 11 (2003) 173.
