Abstract

Residual stresses play a significant role in the overall part quality of additively manufactured (AM) parts. These stresses are the result of complex thermo-visco-mechanical conditions on the part surface (layer surface) during the AM process. Presence of residual stresses within the part may lead to unfavorable consequences like premature fatigue failure and distortions in the part geometry. Residual stress modeling (RSM) is, therefore, an important aspect of AM research. The initial efforts of this research will be geared towards the preparation of multiscale internal state variable (ISV) model based on a preexisting recrystallization ISV Constitutive model calibrated for the α and β phase Ti6Al4V alloy. A transient study of the heat transfer and fluid flow characteristics in the melt pool, based on the first principles and laser parameters will give the necessary temperature field for the numerical evaluation of the residual stresses. The final goal of this research is to set up a framework for RSM modeling for different metallic materials across various AM methods.

Introduction

Additive manufacturing (AM) has been widely used over the past few years in the fabrication of complex functional parts. The process employs automated machines that utilize a spliced CAD file to systematically heat, melt and solidify raw material (usually in the form of a powder), till a functional part is produced. The part is generated in a layer by layer manner in the presence of a moving heat source such as a laser or an electron beam.^[1][2] The process results in the fabrication of functional parts of complex geometries and near net shape. Costs associated with retooling and assembly are completely avoided with additive manufacturing, resulting in a flexible process capability. The various AM techniques can be broadly classified into two types based on powder deposition: powder bed fusion (PBF) and director energy deposition (DED).^[3] Since AM processes are still relatively new to the manufacturing industry, extensive research is being conducted to address certain challenges to the field. Among the literature, most of the topics focus on AM machine parameters influence on material densification, microstructure evolution, and mechanical properties.^[4][5][6][7] Other important issues are the residual stresses and distortion effects, which degrade the build quality of the AM fabricated parts. The presence of the residual stresses in AM parts is due to the spatially varied complex temperature field. The magnitude of these stresses can sometimes exceed the yield strength of the alloy leading to poor fracture toughness, corrosion resistance, and premature fatigue failure. The presence of residual stresses along in part thickness direction can result in delamination and buckling. Distortion effects due to high cyclic temperature fields may hinder dimensional accuracy.^[8]

Experimental measurements of stresses and strains for fabricated parts are expensive and time-consuming. This is because the AM process has many process variables that influence individual part quality. Earlier efforts by other authors in RSM and distortion modeling yielded some interesting observations. Ghosh et al. found that the microstructural changes within the deposited material influenced the distortion results obtained by their numerical model.^[9] Moreover, the high temperatures attained during the deposition process caused the material to anneal.^[10] Since annealing involves recovery and recrystallization, the residual stresses in the fabricated part could be significantly lower. If the annealing effects are not considered, the numerical model will overpredict the overall residual stresses within the part. To counteract the annealing effects, Song et al. resorted to plastic strain relaxation by selecting a critical temperature to set the plastic strain values to zero.^[11] Other efforts in the field of RSM and distortion modeling are also worth noting. Denlinger et al. performed RSM on electron beam manufactured Ti6Al4V by relaxing the elastic, plastic and equivalent plastic strains and stress at the previous increment to zero.^[12] Robinson et al. developed an effective scan strategy combined with non-destructive diffraction methods to reduce residual stresses for powder bed processes.^[13] Le Roux et al. found a novel way of assessing the residual stresses in SLM by improving on the bridge curvature method.^[14] Ahmad et al. used the contour method on the SLM manufactured Ti64 and Inconel 718 for the purpose of residual stress evaluation. They were able to locate the nature of residual stresses at the locations of the part surface. They were able to achieve correlation between the contour method and numerical method.^[15] And finally, Bartlett et al. studied the mechanism of residual stress development in AM via the DIC technique and the RS emerged from sequential reheating and cooling of the new surface and changed dynamically between layers.^[16]

The aim of the current research is to develop a robust multiscale ISV model that can provide accurate constitutive equations. The material data can be accurately obtained only if the model can account for the complex static and dynamic recrystallization and recovery associated with annealing along with creep associated with thermomechanical deformation. To that end, the existing unified static and dynamic recrystallization ISV model by Cho et al.^[17] is calibrated for Ti6Al4V material (α and β phase). This is done by utilizing the ICME multiscale approach. Once, the model is calibrated, the material data generated by the model can be used in the FEA simulations in conjunction to the transient temperature field obtained from first principle analysis of heat transfer and fluid flow problem of the melt pool with a specific laser source. The usage of the ISV model allows us to consider complex physical phenomena such as phase transformation and creep effects. The critical stress relaxation temperature Tcrit is observed state variable (OSV) and can be found out by performing the inverse simulation. An important consideration of the analysis is the boundary conditions. The part is deposited onto the substrate which remains fixed. The main mode of heat transfer during the AM process when the material is in the liquid state is the convective heat transfer in the liquid metal. Heat transfer occurs out of the part by convection radiation to surroundings. To account for the convective heat transfer in the liquid metal, the Marangoni stress condition is used.^[18] The elastic, plastic and equivalent plastic strains along with the stress from the previous increment will be subjected to relaxation once the critical temperature is attained. The stress profiles obtained at the end of the analysis will be verified against experimental data.

ICME Approach

To adopt the ICME ^[19] approach for the problem, the annealing effects observed during the part fabrication need to be captured in the constitutive material behavior. Then, the material data for elastic and plastic deformation and the hardening behavior of the material were considered. It was also realized that the critical temperature for annealing to take place is an OSV and hence must be obtained from inverse simulations. In view of the mentioned considerations, a flowchart was made before the ISV model selection.

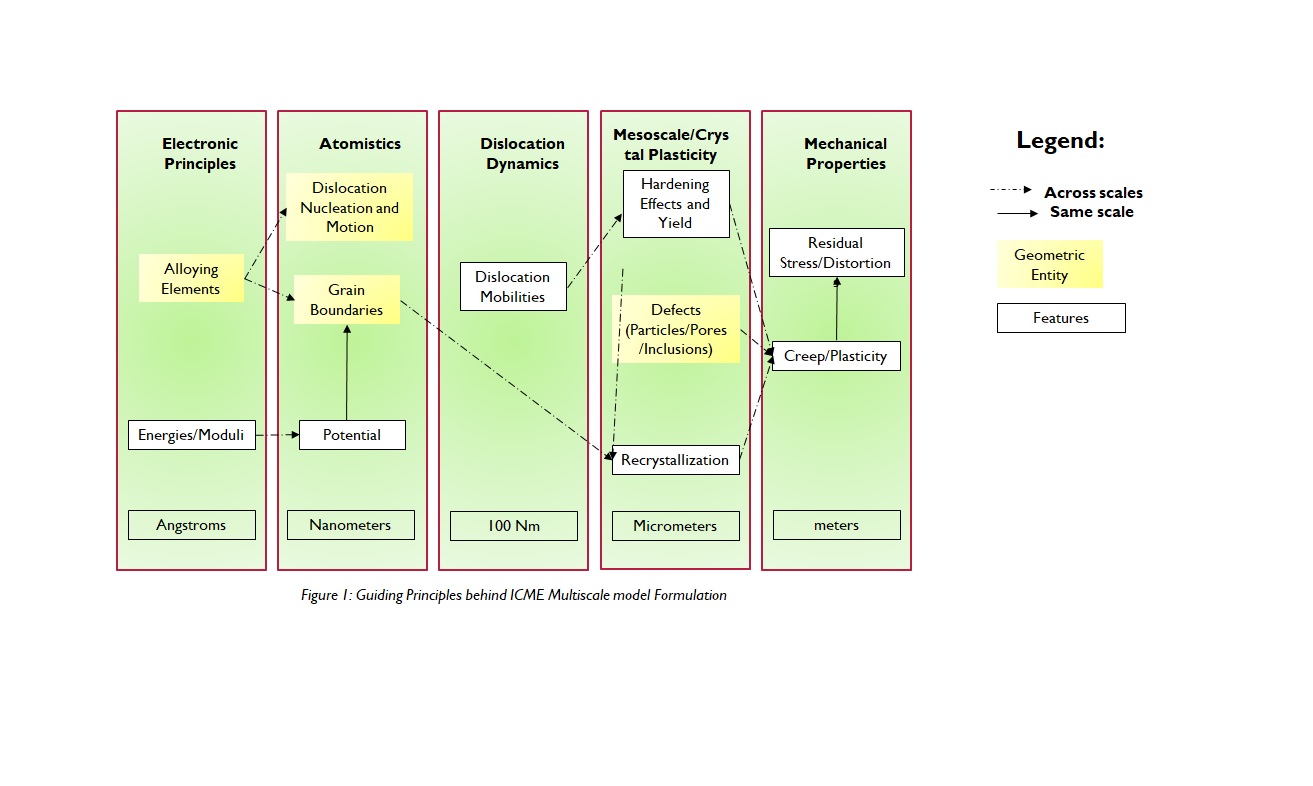
The unified static and dynamic recrystallization Macro ISV model was developed by Cho et al.^[17] was selected based on the guiding principle flowchart.

Downscaling

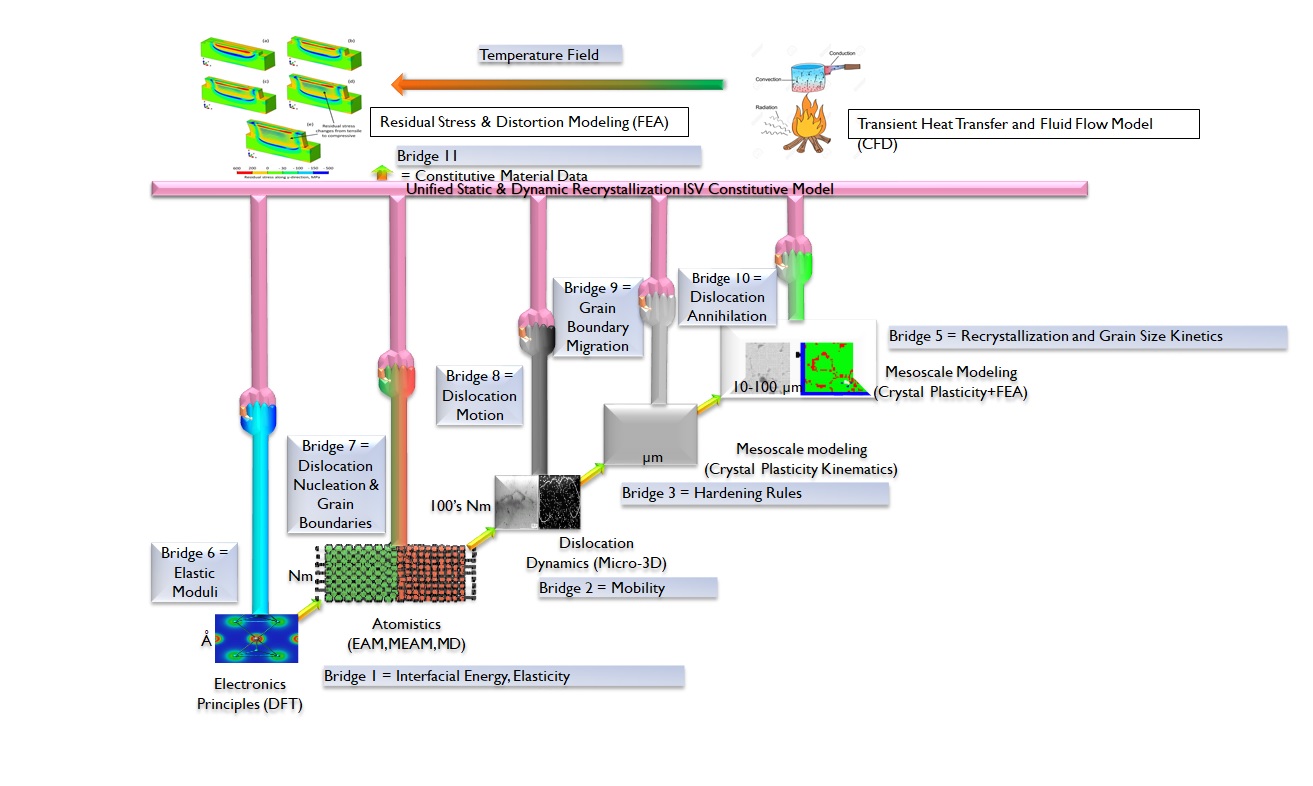
The downscaling requirements of the higher scale models were evaluated to initialize the ICME process. This is done to conduct appropriate simulations at the lower scales to get the input that must be supplied to the higher scales. The RSM-FEA at the structural scale needs the material data, plasticity behavior from the ISV model. The ISV model, in turn, gets the bulk and elastic moduli from the DFT (electronics principles) calculations {Bridge 6}. It also requires recrystallization and plasticity parameters from the lower scales. These are supplied from the Nano and micro scales. The first of the annealing contributions are given by the MD and EAM calculations in the Nanoscale {Bridge 7}. The plasticity parameters are fed into the ISV model through dislocation dynamics and mesoscale modeling of crystal plasticity in the microscale {bridges 8 and 9}. The annealing effects are categorized into static and dynamic recovery and recrystallization phases. During the recovery phase, we see signs of dislocation annihilation and grain boundary migrations resulting in the signs for grain growth {bridge 9}.

Upscaling

This step involved the importing of relevant information from the lower length scales. The DFT calculations are implemented on the electronic scale to obtain elastic properties, GSFE, coherence properties. These properties are used to create a MEAM potential, which will be used to generate dislocation velocity, the drag coefficient, and dislocation mobility through dislocation dynamics. The hardening laws are then obtained in the mesoscale. These are incorporated as material data in the ISV and RSM FEA while being used to develop a pair potential for the MEAM for dislocation mobility and nucleation. The ISV model uses conjugate pairing type relationship between stress and strain. In the case of recrystallization:

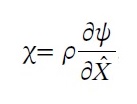
Where χ is a stress-type quantity arising from the recrystallization process and is X the strain-like quantity associated with recrystallized volume fraction.^[17] The various hardening rules will be upscaled to obtain recrystallization parameters. Figure 2 shows the complete bridge circuit for the ICME framework.

Conclusion

Based on the Bridge circuit constructed, the Multiscale ISV model will have to be calibrated for α & β phase Ti6Al4V. The internal state variables in this model have been selected through the process of optimization of characteristics through genetic algorithms. The technique will be studied to bring material or phase-specific changes to the model if required. The constitutive data on annealing and other material data will explain the complex relationship of the material with the melt pool conditions and hence can be accurately used to model the Residual stress profile based on the evaluated transient temperature field in the presence of appropriate boundary conditions and by employing the stress relaxation techniques to account for annealing effects.

References

1. ↑ D.D. Gu, W. Meiners, K. Wissenbach, R. Poprawe, "Laser additive manufacturing of metallic components: materials, processes and mechanisms.," Int. Mater. Rev., pp. 133-164, 2012.
2. ↑ W.J. Sames, F.A. List, S. Pannala, R.R. Dehoff, S.S. Babu, "The metallurgy and processing science of metal additive manufacturing.," Int. Mater. Rev, pp. 1-46, 2016.
3. ↑ C. Li, Z.Y. Liu, X.Y. Fang, Y.B. Guo, "Residual Stress in Metal Additive Manufacturing," in 4th CIRP Conference on Surface Integrity (CSI 2018), 2018.
4. ↑ J.P. Kruth, G. Levy, F. Klocke, T.H.C. Childs, "Consolidation phenomena in laser and powder- bed based layered manufacturing," CIRP Ann. Manuf. Technol, vol. 56, no. 2, pp. 730-759, 2007.
5. ↑ M. Simonelli, Y.Y. Tse, C. Tuck, "Effect of the build orientation on the mechanical properties and fracture modes of SLM Ti–6Al–4V," Mater. Sci. Eng. A, pp. 1-11, 2014.
6. ↑ Y.J. Liu, S.J. Li, H.L. Wang, W.T. Hou, Y.L. Hao, R. Yang, T.B. Sercombe, L.C. Zhang, "Microstructure, defects and mechanical behavior of beta-type titanium porous structures manufactured by electron beam melting and selective laser melting," Acta Mater., vol. 113, pp. 56-67, 2016.
7. ↑ S. Leuders, M. Thöne, A. Riemer, T. Niendorf, T. Tröster, H.A. Richard, H.J. Maier, "On the mechanical behavior of titanium alloy TiAl6V4 manufactured by selective laser melting: fatigue resistance and crack growth performance," Int. J. Fatigue, vol. 48, pp. 300-307, 2013.
8. ↑ T. Mukherjee, W. Zhang, T. DebRoy, "An improved prediction of residual stresses and distortion in additive manufacturing," Computational Materials Science, vol. 126, pp. 360-372, 2017.
9. ↑ Ghosh S, Choi J, "Three-dimensional transient finite element analysis for residual stresses in the laser-aided direct metal/material deposition process," J Laser Appl, pp. 17-144, 2005.
10. ↑ Griffith M, Schlienger M, Harwell L, "Thermal behavior in the LENS process.," in Proceedings of the solid freeform fabrication symposium, Austin, TX, 1998.
11. ↑ Song X, XieM, Hofmann F, et al, "Residual stresses and microstructure in powder bed direct laser deposition (PB DLD) samples," Int J Mater Form, vol. 10, pp. 1-10, 2014.
12. ↑ Denlinger, Erik R., "Residual Stress and Distortion Modeling of Electron Beam Direct Manufacturing Ti-6Al-4V," Journal of Engineering Manufacture, vol. 229.10, pp. 1803-1813, 2015.
13. ↑ J. Robinson, I. Ashton⁎, P. Fox, E. Jones, C. Sutcliffe, "Determination of the effect of scan strategy on residual ff stress in laser powder bed fusion additive manufacturing," Additive Manufacturing, vol. 23, pp. 13-24, 2018.
14. ↑ Sabine Le Roux, Mehdi Salem, Anis Hor, "Improvement of the bridge curvature method to assess residual stresses in selective laser melting," Additive Manufacturing, vol. 22, pp. 320-329, 2018.
15. ↑ Bilal Ahmad, Sjoerd O. van der Veen, Michael E. Fitzpatrick, Hua Guo, "Residual stress evaluation in selective-laser-melting additively manufactured titanium (Ti-6Al-4V) and Inconel 718 using the contour method and numerical simulation," Additive Manufacturing, vol. 22, pp. 571-592, 2018.
16. ↑ Jamison L. Bartlett, Brendan P. Croom, Jeffrey Burdick, Daniel Henkel, Xiaodong Li, "Revealing mechanisms of residual stress development in additive manufacturing via digital image correlation," Additive Manufacturing, vol. 22, pp. 1-12, 2018.
17. ↑ H.E. Cho, Y. Hammi, A.L. Bowman, Shun-Ichiro Karato, J.R. Baumgardner, M.F. Horstemeyer, "A unified static and dynamic recrystallization Internal State Variable (ISV) constitutive model coupled with grain size evolution for metals and mineral aggregates," International Journal of Plasticity, vol. 112, pp. 123-157, 2019.
18. ↑ A. Raghavan, H.L. Wei, T.A. Palmer, T. DebRoy, "Heat transfer and fluid flow in additive manufacturing," J. Laser Appl, vol. 25, 2013.
19. ↑ Mark F. Horstemeyer, Integrated computational materials engineering (ICME) for metals: using multiscale modeling to invigorate engineering design with science., Hoboken, N.J, WILEY-TMS, 2012.