Fig. 1 Amorphous Polymers (from Google image)

Abstract

Modern computational methods have proved invaluable for the design and analysis of structural components using lightweight materials. The challenge of optimizing lightweight materials in the design of industrial components relates to incorporating structure-property relationships within the computational strategy to incur robust designs. One effective methodology of incorporating structure-property relationships within a simulation-based design framework is to employ a hierarchical multiscale modeling strategy. This paper reviews techniques of multiscale modeling to predict the mechanical behavior of amorphous polymers. Hierarchical multiscale methods bridge nanoscale mechanisms to the macroscale/continuum by introducing a set of structure-property relationships. This review discusses the current state of the art and challenges for three distinct scales: quantum, atomistic/coarse graining, and continuum mechanics. For each scale, we review the modeling techniques and tools, as well as discuss important recent contributions. To help focus the review, we have mainly considered research devoted to amorphous polymers.

Why is Amorphous Polymers Mechanical Behavior important?

Many researchers are trying to find ways to save fuel and reducing the cost production. Researchers also want to reduce the amount of money on mechanical test for example like crash test. The different types of material properties prediction for Amorphous Polymer was large range temperature, strain rate, stress states, material microstructure, and molecular mechanisms. But they're still challenges to make this polymer a structural component and that requires a rigorous description of the material behavior from the nanoscale to macroscale.

Different Length Scale

Electronic Scale

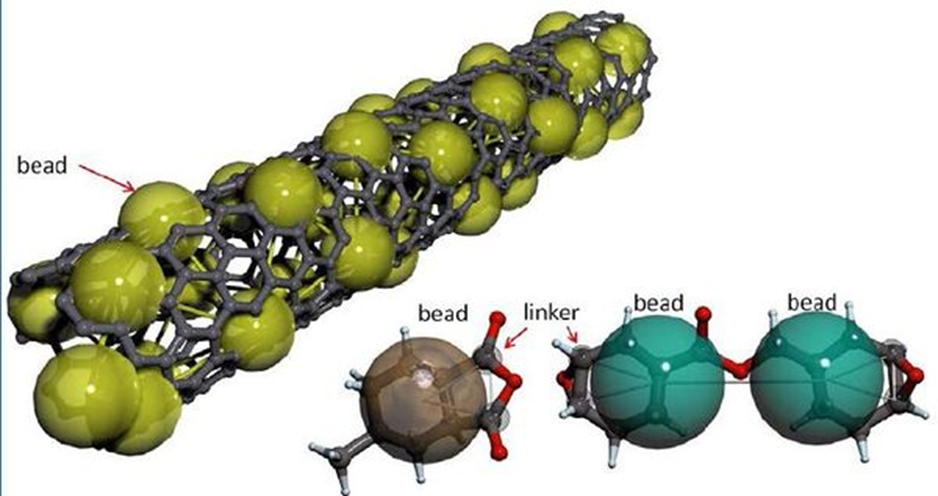
Fig. 2 Polycarbonate bead spring coarse-grain model (google images)

Quantum Mechanics was used to create a method to help with the perform of the molecular simulations. The simulation helped give accurate polymer material properties. DFT (Density Functional Theory) played a big part in Quantum Mechanics. The essential parameters like bond lengths, bond angles, dihedral angles, and force field potentials were the main focus when dealing at this particular length scale. Bisphenol A polycarbonate (BPAPC) was the most important polycorbonates because of its outstanding optical and mechanical properties. This material played an important material for manufacturing and design. There was many studies on polycarbonate structure and energy when using Quantum Mechanics in the 1960s. The main focus was to calculate the ground state conformational energies and ring flips of the phenyl ring. The earlier studies were also used in empirical formulations to develop nonbonded Van der Waals interactions.

Nanoscale

• This particular section used different techniques when using Molecular Dynamics to find the current state of modeling polymer. The most important component in atomic simulations for polymer was the initial position of the particles.
• Interatomic potential was required in MD and to solve this problem
• Mayo et al. create a Dreiding potential used to describe interactions between most nonmetallic elements.
• Van der Waals is way to find out the polarity of intermolecular force between molecules and two different types of Van der Waals force: London Dispersion Forces and dipole-dipole forces
• Molecular theory-collection of particles through time and space by numerically integrating Newton's equation of motion

Micro/Macroscale

This section mainly focus on describing the large deformation kinematics and thermodynamics framework. On the microscopic level, polymers are looked as a discontinuous atomic structure characterized by molecules and large gaps between. While on the Macroscopic level, theories like quantum, Molecular, and atomistic were too computationally expensive for use in solving engineering boundary value problems.,The Kinematics main foundation is based on the Continuum theory and the theory is based on the fundamental assumption that a body. Kinematics also rely on the first law of thermodynamics and the different time scales and length scales. On the Kinematics side, Polymers were characterized when their mechanical properties during large deformations. The deformations would include things like large stretching and/or rotations.

Summary

• This main goal for this article is to develop a new polymer that can help reduce cost, improve safety, ultra lightweight and that can be manufacture. But this type of polymer is on the forefront of design.
• The hierarchical multiscale methods was used to look at the mechanical behavior using the Quantum Mechanic, Molecular Dynamics, and Continuum Mechanic.
  • Quantum Mechanics predicts energies inside a few hundred atoms for the polymer.
  • Molecular Dynamics purpose was to capture elastic and viscous properties of the material. The Molecular Dynamics can also show the deformation mechanisms controlling the motion. The future goal is to develop evolution equations and energetic relation so that it can be pass to Continuum Mechanics.
  • Continuum Dynamics main purpose is to remove the atomistic details of the problem and are used to solve the largest size problems. Continuum model are phenomenological and lack physical meaning
• The study on metals was used as a reference on amorphous polymer

Reference

[1] Bouvard, J.L., Ward, D.K., Hossain, D., Nouranian, S., Marin, E.B. and Horstemeyer, M.F., 2009. Review of hierarchical multiscale modeling to describe the mechanical behavior of amorphous polymers.

[2] https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry) /Physical_Properties_of_Matter/Atomic_and_Molecular_Properties/Intermolecular_Forces/Van_der_Waals_Forces