Abstract

This paper presents the formulation of a constitutive model for amorphous thermoplastics using a thermodynamic approach with physically motivated internal state variables. The formulation follows current internal state variable methodologies used for metals and departs from the spring-dashpot representation generally used to characterize the mechanical behavior of polymers like those used by Ames et al. in Int J Plast, 25, 1495–1539 (2009) and Anand and Gurtin in Int J Solids Struct, 40, 1465–1487 (2003), Anand and Ames in Int J Plast, 22, 1123–1170 (2006), Anand et al. in Int J Plast, 25, 1474–1494 (2009). The selection of internal state variables was guided by a hierarchical multiscale modeling approach that bridged deformation mechanisms from the molecular dynamics scale (coarse grain model) to the continuum level. The model equations were developed within a large deformation kinematics and thermodynamics framework where the hardening behavior at large strains was captured using a kinematic-type hardening variable with two possible evolution laws: a current method based on hyperelasticity theory and an alternate method whereby kinematic hardening depends on chain stretching and material plastic flow. The three-dimensional equations were then reduced to the one-dimensional case to quantify the material parameters from monotonic compression test data at different applied strain rates. To illustrate the generalized nature of the constitutive model, material parameters were determined for four different amorphous polymers: polycarbonate, poly(methylmethacrylate), polystyrene, and poly(2,6-dimethyl-1,4-phenylene oxide). This model captures the complex character of the stress–strain behavior of these amorphous polymers for a range of strain rates.

Constitutive Model

Figures

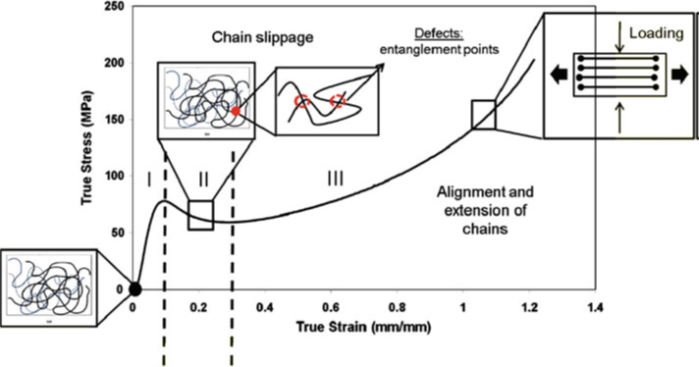
Fig. 1 Response of an amorphous polymer under compression for temperatures below the glass transition temperature

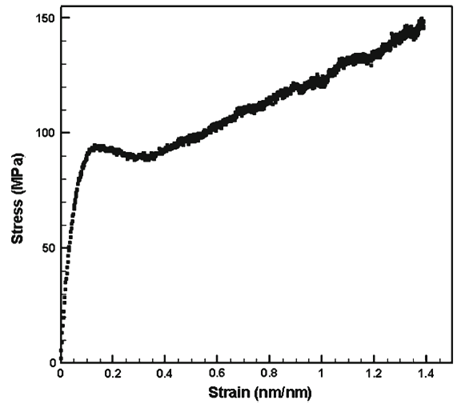
Fig. 2 The stress–strain response for a molecular dynamics simulation consisting of 200 chains with 1,000 monomers/chain at 250K deformed under uniaxial tensile loading and unloading with a strain rate of 109/s

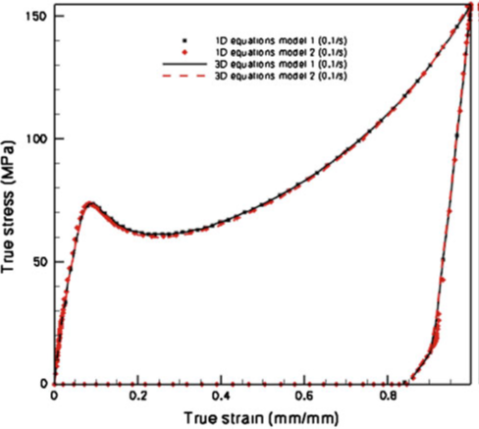
Fig. 3 Comparison of the one-dimensional model results in MATLAB and the constitutive model implemented in ABAQUS

Publication

Bouvard, J.L., Ward, D.K., Hossain, D., Marin, E.B., Bammann, D.J. and Horstemeyer, M.F., 2010. A general inelastic internal state variable model for amorphous glassy polymers. Acta mechanica, 213, pp.71-96. Acta Mechanica 213