CAVS / Capabilities / Materials Modeling / ICME / Bauschinger

Integrated Computational Materials Engineering (ICME)

Atomistic Simulations of Bauschinger Effects of Metals With High Angle and Low Angle Grain Boundaries

Full Citation: H. Fang, M.F. Horstemeyer, M.I. Baskes, K. Solanki "Atomistic simulations of Bauschinger effects of metals with high angle and low angle grain boundaries." Computer methods in applied mechanics and engineering 193.17 (2004): 1789-1802.

Abstract

In this paper, we examined Bauschinger effects in nickel single crystals and nickel containing arrays of high angle or low angle grain boundaries under shear deformation using molecular dynamics with embedded atom method (EAM) potentials. In order to take into account dislocation nucleation under different boundary conditions and their effects on the stress–strain relationship, two limiting constraints were used to both high angle and low angle grain boundaries: fixed end on all sides and free ends on all sides. Stress–strain curves were then compared under these two boundary conditions for three cases: single crystal, high angle grain boundary arrays, and low angle grain boundary arrays. In each of the three cases, loading was reversed at different strain levels after yield and Bauschinger effects were examined on all the scenarios. The simulation results were also compared with macroscopic mechanics ideas for both high angle and low angle grain boundaries. The Bauschinger effect was found to be the largest for the case of high angle boundaries and the lowest for the single crystal.

Methodology

Stress-strain responses for Nickel were studied for single crystal, low angle grain boundary, and high angle grain boundary models using molecular dynamics with the embedded atom method. Forward and reverse simple shear load was applied with fixed and flexible end boundaries for all three models. The stress-strain responses and Bauschinger effect were studied for the three models for both fixed and flexible boundaries.

Results

The single crystal model showed the smallest Bauschinger effect, while the high angle grain boundary model showed the largest for both fixed and flexible end boundaries. The low angle grain boundary model exhibited dislocation nucleation earlier than the single crystal and high angle grain boundary models for both boundaries; dislocation nucleation occurred before the apparent yield for the low angle model, while the single crystal and high angle models did not undergo dislocation nucleation until after the apparent yield.

Acknowledgements

The work by Fang, Horstemeyer, and Solanki was sponsored by the Mississippi State University Center for Advanced Vehicular Systems, and the work by Baskes has been sponsored by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Materials Sciences. We would like to thank Dr. B. Zhang, Department of Mechanical Engineering, Mississippi State University, for his valuable comments and discussions on the work presented in this paper.

Select Figures

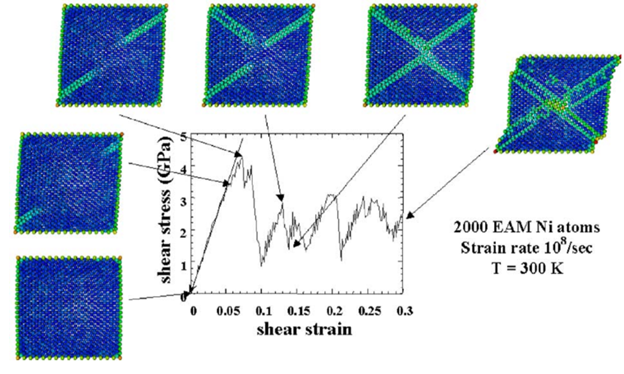
Shear strain graph with blue squares

Figure 4: Evolution of dislocations for single crystal nickel relative to volume averaged stress-strain response

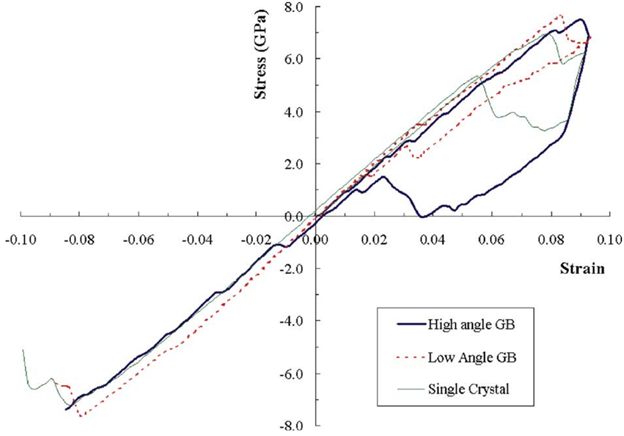
volume with 9% strain

Figure 7: Volume averaged stress-strain response for fixed-end, reverse loading at 9% strain

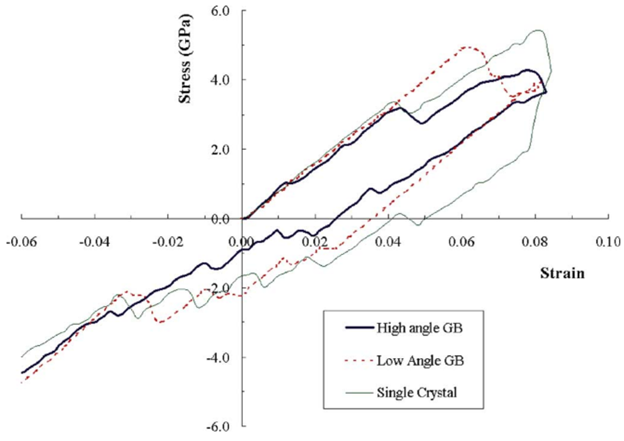
volume with 8% strain

Figure 8: Volume averaged stress-strain response for flexible-end, reverse loading at 8% strain

References

  1. P.M. Gullett, M.F. Horstemeyer, D.J. Bammann, and M.I. Baskes, A comparison of atomistic and elastic continuum based shear stress distributions near an edge dislocation, in: Proceedings of the International Conference on Computational Engineering and Science, August 19–25, 2001, Puerta Vallarta, Mexico.
  2. M.F. Horstemeyer, and M.I. Baskes, Strain tensors at the atomic scale, MRS in: Proceedings of Multiscale Phenomena in Materials: Experiments and Modeling, vol. 578, Pittsburgh, PA, 2000.
  3. M.F. Horstemeyer, M.I. Baskes, D.A. Hughes, A. Godfrey, Orientation effects on the stress state of molecular dynamics large deformation simulations, Int. J. Plasticity 18 (2002) 203–209.
  4. K.A. Gall, M.F. Horstemeyer, M. Van Schilfgaarde, M.I. Baskes, Atomistic simulations on the tensile debonding of an aluminum–silicon interface, J. * Mech. Phys. Solids 48 (2000) 2183–2212.
  5. W.W. Gerberich, N.I. Tymak, J.C. Grunlan, M.F. Horstemeyer, M.I. Baskes, Interpretations of indentation size effects, J. Appl. Mech. 69 (2002) 442–443.
  6. M.F. Horstemeyer, S.J. Plimpton, M.I. Baskes, Size scale and strain rate effects on yield and plasticity of metals, Acta Mater. 49 (2001) 4363–4374.
  7. M.F. Horstemeyer, M.I. Baskes, S.J. Plimpton, Computational nanoscale plasticity simulations using embedded atom potentials, Theor. Appl. Fract. Mech. 37 (2001) 49–98.
  8. M.F. Horstemeyer, T.J. Lim, W.Y. Lu, D.A. Mosher, M.I. Baskes, V.C. Prantil, S.J. Plimpton, Torsion/simple shear of single crystal copper, J. Engrg. Mater. Technol. 124 (2002) 322–328.
  9. M.S. Daw, M.I. Baskes, Embedded-tom method: derivation and application to impurities, surfaces, and other defects in metals, Phys. Rev. B (1984) 6443–6453.
  10. J. Freidel, Phil. Mag. 43 (1952) 153.
  11. M.J. Stott, E. Zaremba, Quasi atoms: An approach to atoms in nonuniform electronic systems, Phys. Rev. B 22 (1980) 1564–1583.
  12. M.S. Daw, S.M. Foiles, M.I. Baskes, The embedded-atom method: a review of theory and applications, Materials Science Reports, A Review Journal 9 (1993) 251–310.
  13. J.E. Angelo, N.R. Moody, M.I. Baskes, Trapping of hydrogen to lattice defects in nickel, J. Model. Simul. Mater. Sci. Engrg. 3 (1995) 289–307.
  14. M.I. Baskes, X. Sha, J.E. Angelo, N.R. Moody, Comment: trapping of hydrogen to lattice defects in nickel, Model. Simul. Mater. Sci. Engrg. 5 (1997) 651–652.
  15. C. Kelchner, S. Plimpton, Hamilton, Dislocation nucleation and defect structure during surface indentation, J. Phys. Rev. B 58 (1998) 11085–11088.
  16. M.F. Horstemeyer, M.I. Baskes, Atomistic finite deformation simulations: a discussion on length scale effects in relation to mechanical stresses, J. Engrg. Matls. Techn. Trans. ASME 121 (1998) 114–119.
  17. M.F. Horstemeyer, Damage influence on Bauschinger effect of a CAST A356 alluminum alloy, Scripta Mater. 39 (1998) 1491–1495.
  18. M.G. Stout, A.D. Rollett, Large-strain Bauschinger effects in FCC metals and alloys, Metall. Trans. A (1990) 3201–3213.
  19. B.K. Chuna, J.T. Jinna, J.K. Lee, Modeling the Bauschinger effect for sheet metals, part II: theory, Int. J. Plasticity 18 (2002) 571–595.
  20. B.K. Chuna, J.T. Jinna, J.K. Lee, Modeling the Bauschinger effect for sheet metals, part II: applications, Int. J. Plasticity 18 (2002) 597–616.
  21. S. Nose, Molecular dynamics simulations, Progr. Theor. Phys. Suppl. 103 (1991) 117.