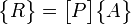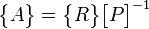Integrated Computational Materials Engineering (ICME)
A Mesomechanics Parametric Finite Element Study of Damage Growth and Coalescence in Polymers Using an Elastoviscoelastic-Viscoplastic Internal State Variable Model
Abstract
A split-level factorial design of experiments (DOE) parametric study using a two-dimensional mesoscale Finite Element Analysis (FEA) was executed to elicit the most essential aspects pertaining to void/crack growth and void/crack coalescence in polymers above the glass transition temperature. The FEA was coupled to a physically based, strain rate and temperature dependent, elastoviscoelastic-viscoplastic internal state variable polymer model that was calibrated to physical experiments. The DOE method examined the relative influences of seven independent parameters related to mechanics (stress state, strain rate, and temperature) and materials science (polymer blend, number of initial defects, defect type, and initial microporosity—also called the subscale free volume) with respect to both void/crack growth and void/crack coalescence in polymers. The results of the DOE algorithm clearly illustrated that the stress state and applied strain rate were the most critical factors affecting void/crack growth. For void/crack coalescence, the stress state and number of defects were the crucial parameters. The conclusions of this study gives insight for the development of a macroscale damage model for polymers.
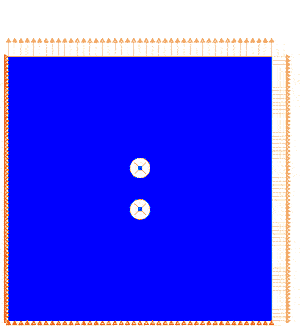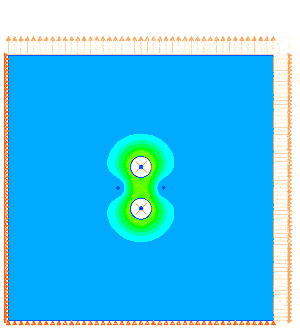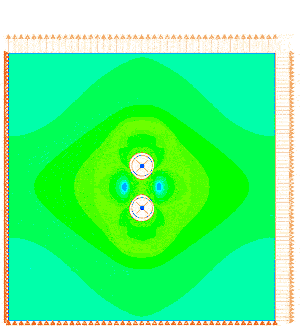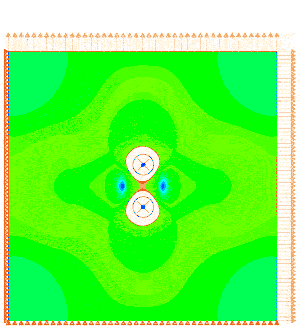
Biaxial loading of a 9x9 mm Polycarbonate plate with 2 defects showing interacting stress fields.
Authors
W. B. Lawrimore II, D. K. Francis, J. L. Bouvard, Mark F. Horstemeyer
Publication
Methodology
This study compares the relative parametric influences between the chosen parameters on damage growth and coalescence in polymers. Having seven parameters quantified at two levels yields 128 (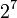 ) unique simulations (one for each possible parameter grouping). The DOE technique is essentially a tool that selects a minimum spanning set for the simulation space based on some criteria. The DOE method creates a linear mapping from a set of influences, {A}, to a set of responses, {R}, through a parameter matrix, {P} corresponding to the orthogonal array with
) unique simulations (one for each possible parameter grouping). The DOE technique is essentially a tool that selects a minimum spanning set for the simulation space based on some criteria. The DOE method creates a linear mapping from a set of influences, {A}, to a set of responses, {R}, through a parameter matrix, {P} corresponding to the orthogonal array with
where:
By inverting the equation, one can solve for {A}:
The Taguchi logarithmic parametric array is shown below:
| Calc | Material | Particle/Void | One/Two Defect(s) | Temperature (K) | Stress State | Strain Rate (1/s) | Microporosity (vol Frac) |
|---|---|---|---|---|---|---|---|
| 1 | ABS | Void | One | 253 | Uniaxial | 0.001 | 0 |
| 2 | ABS | Void | One | 323 | Biaxial | 0.1 | 0.001 |
| 3 | ABS | Particle | Two | 253 | Uniaxial | 0.1 | 0.001 |
| 4 | ABS | Particle | Two | 323 | Biaxial | 0.001 | 0 |
| 5 | PC | Void | Two | 253 | Biaxial | 0.001 | 0.001 |
| 6 | PC | Void | Two | 323 | Uniaxial | 0.1 | 0 |
| 7 | PC | Particle | One | 253 | Biaxial | 0.1 | 0 |
| 8 | PC | Particle | One | 323 | Uniaxial | 0.001 | 0.001 |
Material Model
A physically-based, rate and temperature dependent ISV model for polymers developed by Bouvard et al. (2013)[2] was used to accurately represent both ABS and PC. The ISV model was calibrated to physical experiments at a variety of temperatures and strain rates for both materials. The constitutive model features three ISVs to account for inelastic dissipation mechanisms in polymers. 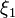 is a strain-like scalar that accounts for dissipation induced from polymer chain entanglement points.
is a strain-like scalar that accounts for dissipation induced from polymer chain entanglement points. 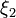 is a strain-like scalar that represents material hardening resulting from polymer chain alignment and coiling at large strains. Lastly,
is a strain-like scalar that represents material hardening resulting from polymer chain alignment and coiling at large strains. Lastly, 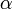 is a strain-like tensor that accounts for hardening induced by polymer chain orientation and stretching at large strains. The ISV model calibrations to physical experiments are shown below.
is a strain-like tensor that accounts for hardening induced by polymer chain orientation and stretching at large strains. The ISV model calibrations to physical experiments are shown below.
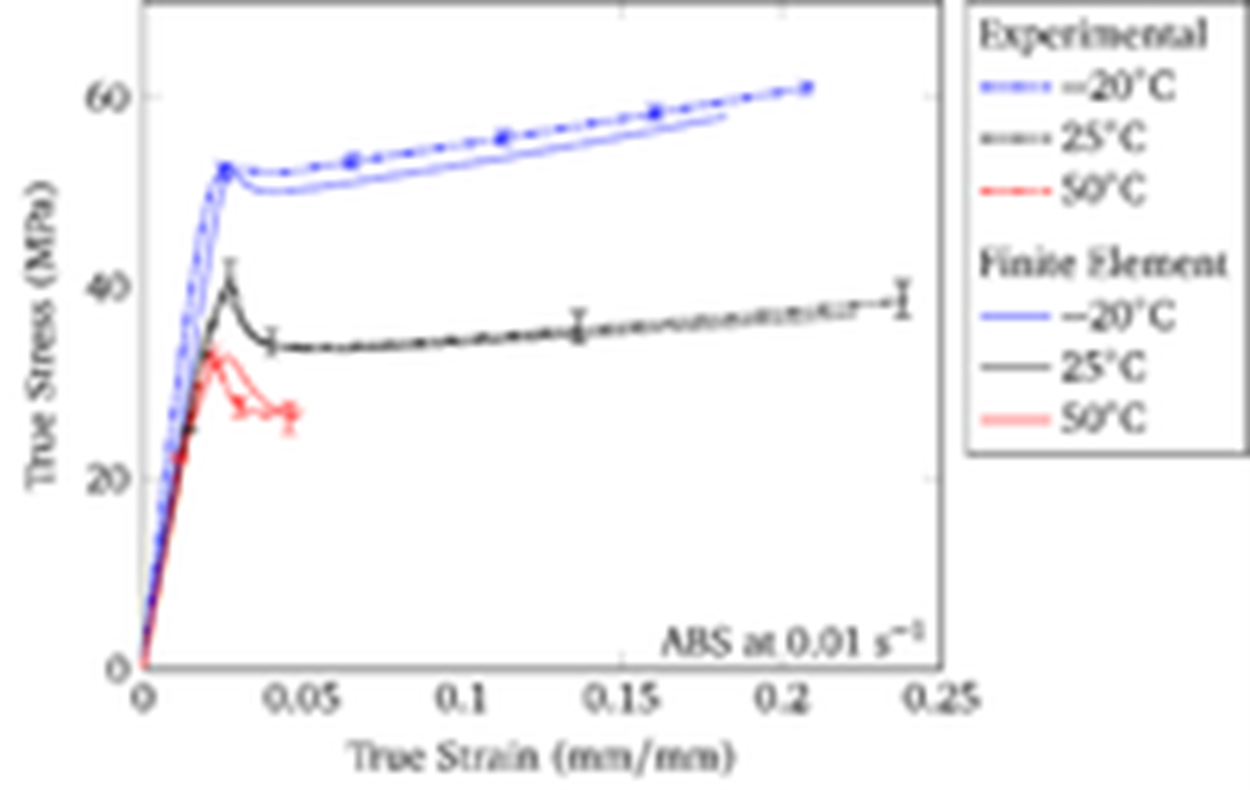
True stress–true strain curves under tension comparing the thermoplastic internal state variable model over a range of temperatures with experiments for acrylonitrile butadiene styrene (ABS).
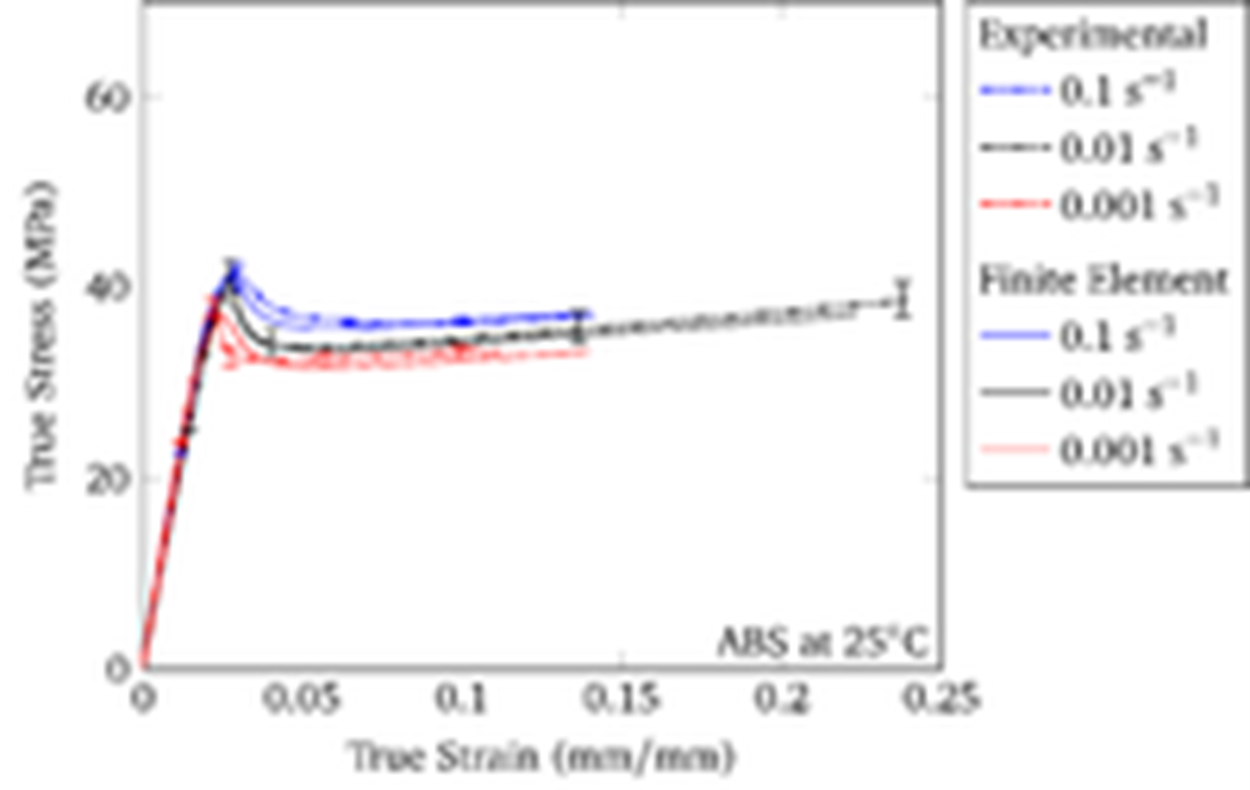
True stress–true strain curves under tension comparing the thermoplastic internal state variable model over a range of strain rates with experiments for acrylonitrile butadiene styrene (ABS).
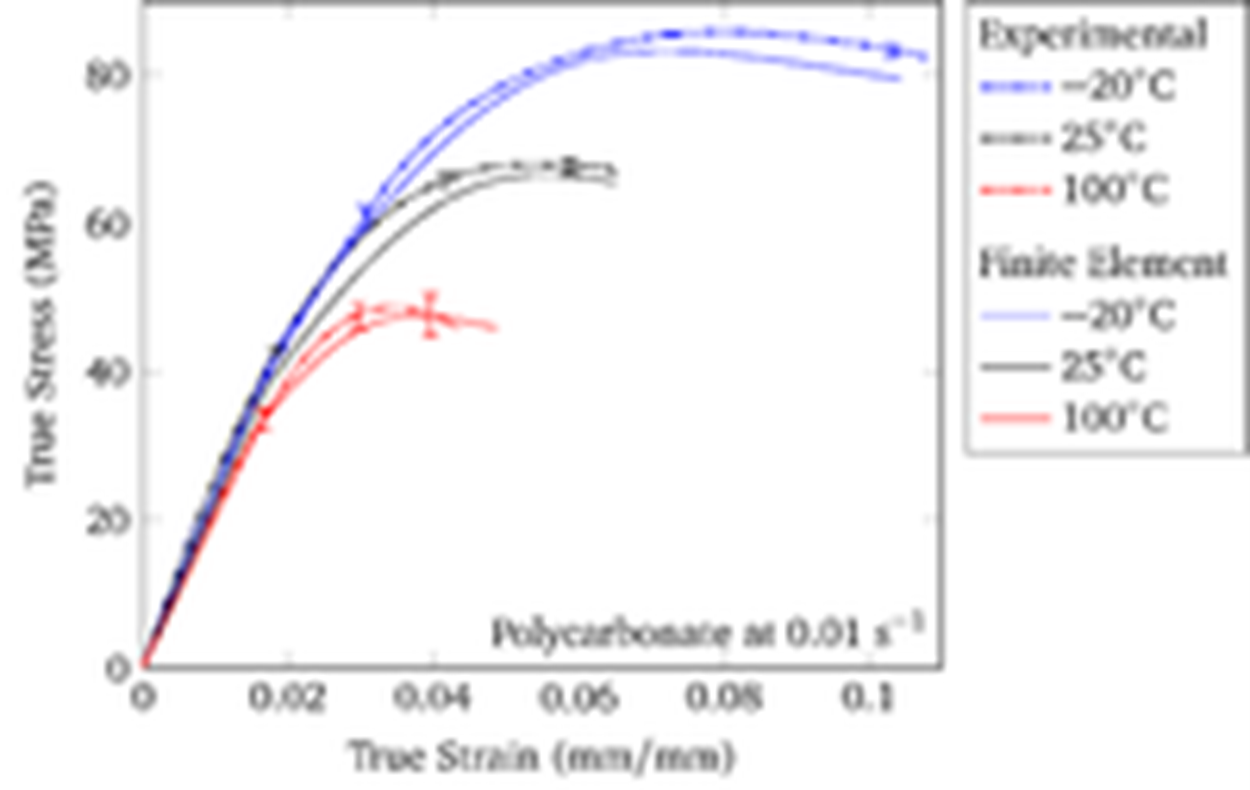
True stress–true strain curves under tension comparing the thermoplastic internal state variable model over a range of temperatures with experiments for polycarbonate (PC).
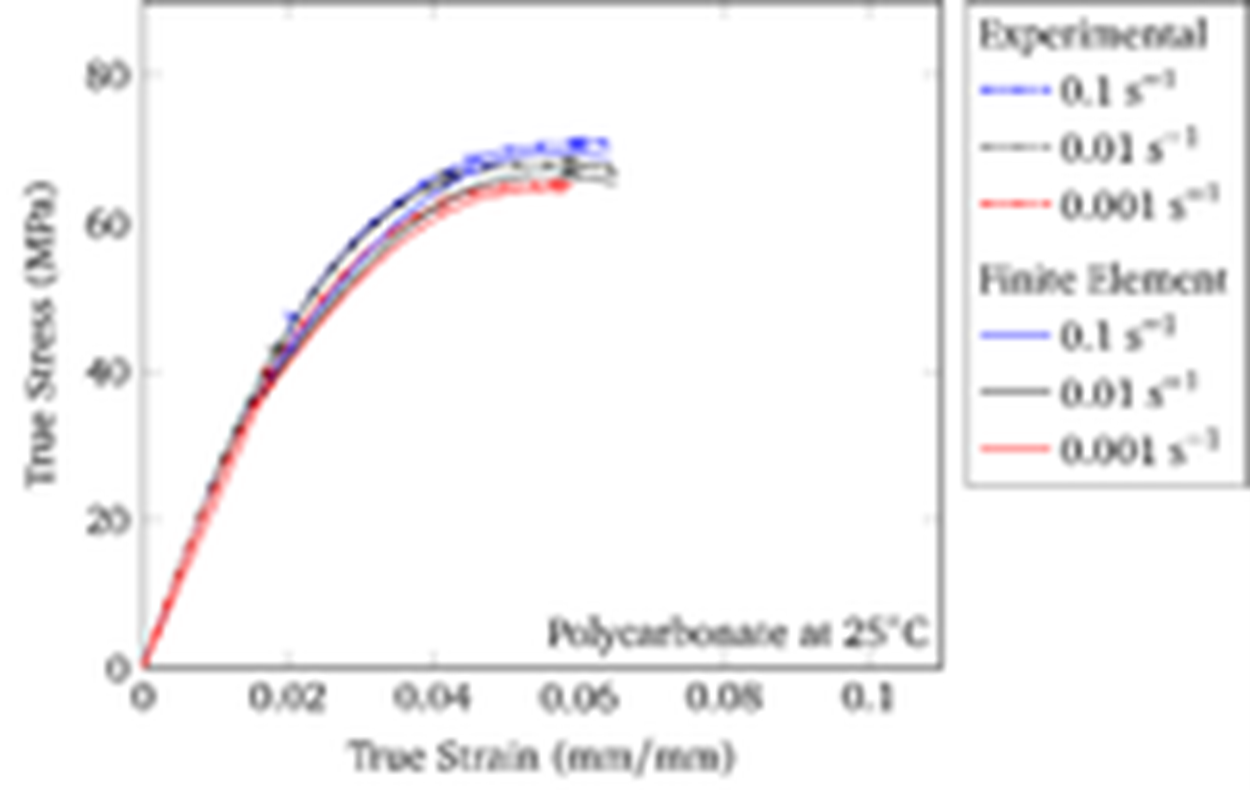
True stress–true strain curves under tension comparing the thermoplastic internal state variable model over a range of strain rates with experiments for polycarbonate (PC).
Finite Element Results

Stress triaxiality contour plots from each design of experiments finite element computations at the peak load.
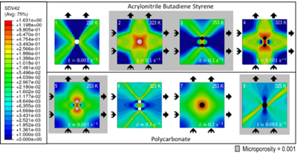
Schematic showing equivalent inelastic strain (SDV42) contour plots for each design of experiments simulation at the peak load.
Parametric Results
Normalized influence of each design of experiments parameter on the aggregate stress triaxiality.
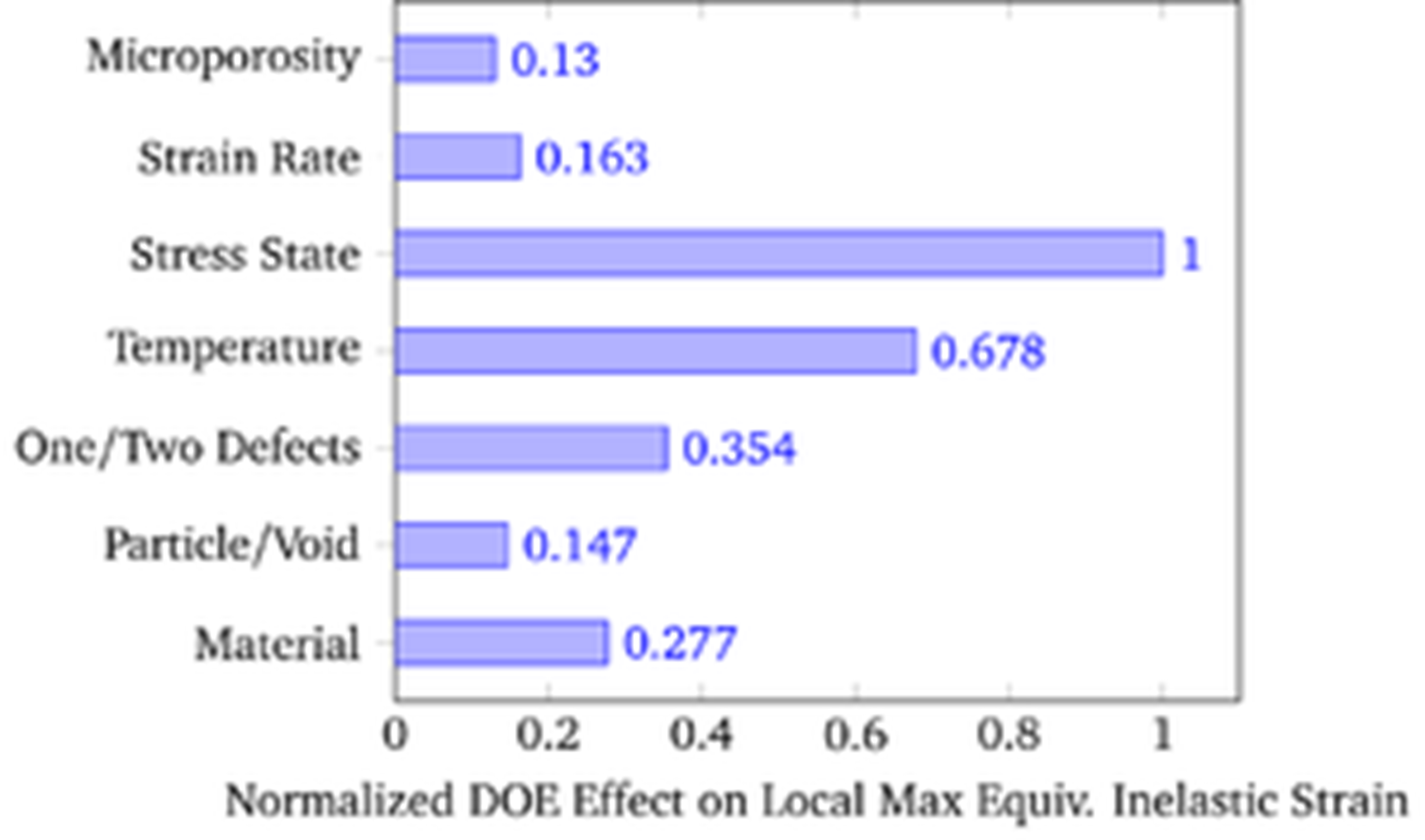
Normalized influence of each design of experiments parameter on the local maximum equivalent inelastic strain.
Normalized influence of each design of experiments parameter on the void volume fraction.
Summary
A DOE parametric study was conducted to discover the crucial influence parameters affecting damage growth and coalescence in polymers. The parametric study employed a finite element analysis coupled with an experimentally calibrated time and temperature sensitive elastoviscoelastic-viscoplastic ISV model for polymers. The analysis revealed that the stress state that induced a particular stress triaxiality was the most important parameter for damage growth. Researchers have argued that viscoelastic materials, such as the structural polymers represented in this study, have a strong strain rate and time sensitivity. Although these polymers do exhibit a strain rate and time sensitivity, the mechanism that induces void growth and coalescence the strongest is a large stress triaxiality arising from an elevated applied stress state with secondary contributions from the material having a larger yield stress and a higher temperature.
References
- W.B. Lawrimore II, D.K. Francis, J.L. Bouvard, Y. Hammi, M.F. Horstemeyer, A mesomechanics parametric finite element study of damage growth and coalescence in polymers using an Elastoviscoelastic-Viscoplastic internal state variable model, Mechanics of Materials, Volume 96, May 2016, Pages 83-95, ISSN 0167-6636
- J.L. Bouvard, D.K. Francis, M.A. Tschopp, E.B. Marin, D.J. Bammann, M.F. Horstemeyer, An internal state variable material model for predicting the time, thermomechanical, and stress state dependence of amorphous glassy polymers under large deformation, International Journal of Plasticity, Volume 42, March 2013, Pages 168-193, ISSN 0749-6419
Licensing
The content of this page was reproduced with permission from Elsevier and Mechanics of Materials License No. 3815371158759